What is Active, Reactive and Apparent Power

Electrical power is a fundamental concept in the realm of electrical engineering, governing the flow of energy from circuits to connected devices. Understanding the different types of power – active, reactive, and apparent – is crucial for ensuring efficient and optimal performance in AC circuits. In this comprehensive article, we will delve deep into the definitions, formulas, and practical implications of these power components, equipping you with the knowledge to navigate the intricate world of electrical power management.

Active Power (P): Actual Power in Use

Active power, also known as real power, is the portion of electrical power that is actively consumed by a circuit and converted into useful work, such as generating heat, light, or mechanical energy. It is measured in watts (W) and represents the actual energy being utilized in the system. Active power is the power that performs the desired tasks and contributes directly to the circuit’s functionality.

The formula for calculating active power is:

P = V × I × cos(θ)

Where:

• P is the active power in watts (W)
• V is the RMS voltage in volts (V)
• I is the RMS current in amperes (A)

cos(θ) is the power factor, which represents the phase angle between voltage and current.

Active power is the energy that is actually consumed in the load, and it is the power produced by a source, such as a generator or battery.

Read More: What is Power Quality, Why is it Important?

Reactive Power (Q):  Key to Sustaining Power Quality

Reactive power, on the other hand, is the alternating current that flows back and forth in an electric circuit. It is the power associated with the energy storage and release due to the presence of inductive or capacitive components, such as inductors and capacitors. The unit used for reactive power is volt-amperes reactive (VAR) or kilovolt-amperes reactive (kVAR).

The formula for calculating reactive power is:

Q = V × I × sin(θ)

Where:

• Q is the reactive power in volt-amperes reactive (VAR)
• V is the RMS voltage in volts (V)
• I is the RMS current in amperes (A)

sin(θ) is the phase angle between voltage and current.

Reactive power does not contribute to performing useful work; instead, it is required to maintain the desired voltage and current levels in the circuit. While reactive power is not directly consumed, it can create inefficiencies and energy losses by increasing the apparent power, leading to a greater flow of current in the circuit.

Apparent Power (S): The Total Demand

Apparent power, also known as complex power or total power, is the total power flowing through an AC circuit, encompassing both the active power and the reactive power. It is measured in volt-amperes (VA) or kilovolt-amperes (kVA) and represents the net power delivered from a source to a line.

The formula for calculating apparent power is:

S = V × I

Where:

• S is the apparent power in volt-amperes (VA)
• V is the RMS voltage in volts (V)
• I is the RMS current in amperes (A)

Apparent power reflects the total power capacity needed in an electrical system, as it accounts for both the real power being used and the reactive power required to maintain voltage levels. While active power directly contributes to performing tasks, apparent power is the measure that determines the size or rating of individual components in the circuit.

Read More: Harmonic Filters | The Key to a Healthy Power Grid

The Relationship Between Active, Reactive, and Apparent Power

The relationship between active, reactive, and apparent power can be summarized as follows:

Active power (P) is the portion of electrical power that is consumed and converted into useful work.

Reactive power (Q) is the power associated with the energy storage and release in the circuit due to inductive and capacitive components.

Apparent power (S) is the total power flowing through the circuit, encompassing both active and reactive power.

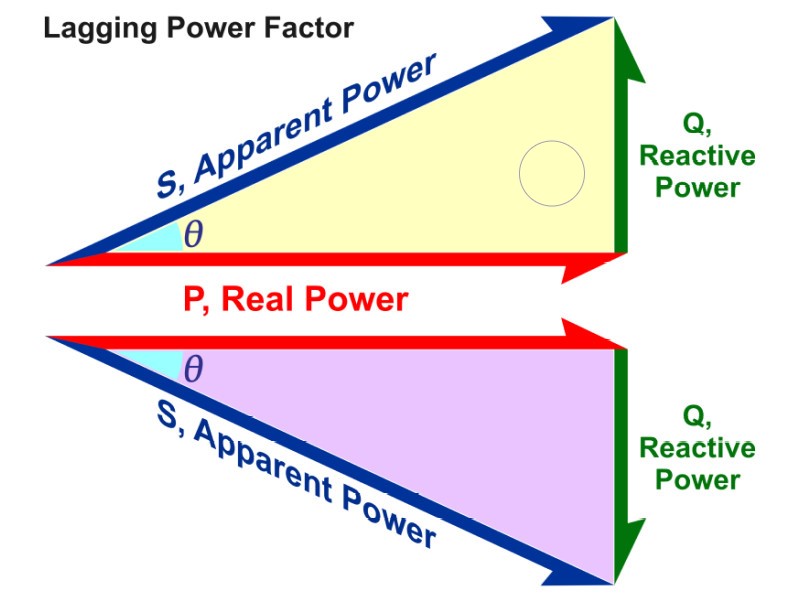
The mathematical relationship between these three power components can be expressed using the Pythagorean theorem:

S² = P² + Q²

This equation demonstrates that the apparent power is always greater than or equal to the active power, as the reactive power contributes to the overall power demand in the circuit.

Power Factor: The Efficiency Indicator

The power factor (cos(θ)) is a crucial parameter that reflects the efficiency with which reactive energy can be exchanged and the amount of unwanted reactive energy that must be absorbed in the circuit. A high power factor indicates that the circuit’s capability for absorbing reactive energy closely matches its ability to utilize active power, resulting in higher efficiency.

The power factor can be calculated as:

Power Factor = Active Power (P) / Apparent Power (S)

or

Power Factor = cos(θ)

A power factor closer to 1 (unity) indicates a more efficient circuit, as it means a larger portion of the apparent power is being used for useful work. Conversely, a lower power factor suggests a less efficient circuit, with a higher proportion of reactive power compared to active power.

Read More: Origin of Electric Frequencies And The Use of 50 Hz and 60 Hz

Importance of Reactive Power Management

While reactive power does not contribute directly to useful work, it is essential for maintaining proper voltage and current levels in the circuit. Excessive reactive power can lead to several issues, including:

Increased current flow: Reactive power increases the total current flowing through the circuit, which can result in higher energy losses and the need for larger-capacity electrical components.

Voltage regulation problems: Reactive power can cause voltage fluctuations, leading to potential instability and impacting the performance of connected devices.

Energy Efficiency: The presence of reactive power reduces the overall efficiency of the electrical system, as more energy is required to maintain the desired power levels.

Effective management of reactive power is crucial for optimizing the performance and efficiency of AC circuits. This can be achieved through the use of power factor correction techniques, such as the installation of capacitor banks or the deployment of synchronous condensers, which help to compensate for the reactive power and improve the overall power factor.

Applications and Implications

The understanding of active, reactive, and apparent power has far-reaching implications in various electrical engineering applications, including:

Power Transmission and Distribution: Knowing the different power components helps in the design and operation of power transmission and distribution systems, ensuring energy efficiency transfer and minimizing losses.

Motor and Generator Design: Accurate calculations of active, reactive, and apparent power are essential for the proper sizing and selection of electric motors and generators, as well as for optimizing their performance.

Energy Efficiency Assessments: Analyzing the power factor and the relationship between active, reactive, and apparent power can help identify opportunities for improving energy efficiency in industrial, commercial, and residential settings.

Electrical System Design : The apparent power is the primary factor in determining the required capacity of electrical components, such as transformers, switchgear, and conductors, to ensure they can handle the total power demand.

Power Quality Improvement: Addressing reactive power issues through power factor correction techniques can help improve power quality, reduce energy costs, and extend the lifespan of electrical equipment.

By understanding the nuances of active, reactive, and apparent power, electrical engineers and technicians can make informed decisions, optimize system performance, and contribute to the overall efficiency and reliability of electrical networks.

Through the effective management of active, reactive, and apparent power, electrical systems can achieve higher efficiency, reduced energy costs, and enhanced reliability, ultimately contributing to the overall sustainability and progress of the electrical industry. As technology continues to evolve, the importance of these power concepts will only grow, making their understanding an essential skill for any electrical professional.

For more articles, follow : https://aktif.net/en/blog/