
Veri Madenciliği Karar Ağaçları
Veri Madenciliği, veri setlerinin sistematik bir analizini içerir ve verilere anlam verir. Veri madenciliği, verilerin toplanması, ayıklanması, işlenmesi, analiz edilmesi ve bunlardan faydalı içgörüler elde edilmesi üzerine yapılan çalışmadır.
Özellikle günümüzde karar ağacı öğrenme algoritması, bilgi yakalamada uzman sistemlerde başarıyla kullanılmaktadır. Bu makalenin amacı, karar ağacı hakkında kısa bir açıklama sunmaktır. Bu makale, karar ağacının anlamını, en iyi bölme kıstası, popüler karar ağacı algoritmalarını, karar ağacının avantajlarını ve dezavantajlarını açıklığa kavuşturmak amacıyla yazılmış olup yazının sonunda ID3/C4.5 uygulanarak bir data seti ele alınmış ve karar ağacı oluşturulmasına yönelik çalışma yapılmıştır. Büyük veri hakkındaki yazımızı okumak için tıklayınız.
Zeynep Ayça Gürel, Elektrik Mühendisi, Kalite Güvence
Giriş
Bu makale karar ağacının ne olduğunu açıklamakta ve karar ağacının veri madenciliğindeki yeri hakkında bilgi vermektedir. Ayrıca, bu makale ağaç boyutu, en iyi bölme kıstası, entropi ve bilgi kazancı hakkında bilgi içermektedir.
Bir örnek kümesinin (veya eğitim kümesinin) sınıfları, yeni örnekler için sınıfları tahmin etmek üzere örneklerin öznitelik vektörünün davranış şeklini keşfetmek için birkaç algoritma kullanabiliriz.
Başlangıçta mantık, yönetim ve istatistikten türetilen karar ağaçları, günümüzde metin madenciliği, bilgi çıkarma, makine öğrenimi ve örüntü tanıma gibi diğer alanlarda oldukça etkili bir araç haline gelmiştir.
Rokach ve Maimon’a göre, Karar ağaçları birçok fayda sağlar:
- Sınıflandırma, regresyon, kümeleme ve özellik seçimi gibi çok çeşitli veri madenciliği görevleri için çok yönlülük
- Kendinden açıklamalı ve takip etmesi açısından kolaylık (sıkıştırıldığında)
- Çeşitli girdi verilerini işleme esnekliği: nominal, sayısal ve metinsel
- Hatalara veya eksik değerlere sahip olabilecek veri kümelerinin işlenmesinde uyarlanabilirlik
- Nispeten küçük bir hesaplama çabasına göre yüksek tahmin performansı
- Çeşitli platformlar üzerinden birçok veri madenciliği paketine uygunluk
- Büyük veri kümeleri için kullanışlılık (bir topluluk çerçevesinde)
Karar ağacı, ID3, C4.5, CART, CHAID, QUEST, Cal5, Fact, LMDT, T1, Public: mars gibi bir öğrenme algoritmasına sahiptir. Bu yazıda bunlardan sadece ikisi açıklanmıştır.: ID3, C4.5.
ID3 algoritması, basitliği nedeniyle bu yazıda uygulama olarak kullanılacaktır.
Karar Ağaçları ile Veri Madenciliği
Aggarwal’a göre, Karar ağaçları, sınıflandırma sürecinin, ağaç benzeri bir yapıda düzenlenmiş, özellik değişkenleri üzerinde bir dizi hiyerarşik karar kullanılarak modellendiği bir sınıflandırma metodolojisidir.
Sharma ve Bhargava & Mathuria’ya göre, Karar ağacı, ağaç benzeri grafik kararları, şans olay sonuçları, kaynak maliyetleri ve yararları dahil olmak üzere bunların olası artçı etkilerini kullanan bir karar destek sistemidir. Bir Karar Ağacı veya bir sınıflandırma ağacı, bağımsız (girdi) niteliklerin (değişkenlerin) değerleri verildiğinde bir bağımlı niteliğin (değişken) değerini sonlandıran bir sınıflandırma işlevini öğrenmek için kullanılır.
Karar ağacı, köklü bir ağaç oluşturan düğümlerden oluşur, yani bu, gelen kenarları olmayan “kök” adı verilen bir düğüme sahip yönlendirilmiş bir ağaçtır. Diğer tüm düğümlerin tam olarak bir gelen kenarı vardır. Dışarı çıkan kenarlara sahip bir düğüme dahili veya test düğümü denir. Diğer tüm düğümlere yapraklar denir (aynı zamanda terminal veya karar düğümleri olarak da bilinir) [3].
Bir karar ağacında, her bir dahili düğüm, giriş öznitelik değerlerinin belirli bir ayrık işlevine göre örnek alanını iki veya daha fazla alt alana böler. En basit ve en sık karşılaşılan durumda, her test tek bir özniteliği dikkate alır, öyle ki örnek alanı özniteliğin değerine göre bölünür. Sayısal öznitelikler söz konusu olduğunda, koşul [3] aralığına atıfta bulunur.
Her yaprak, en uygun hedef değeri temsil eden bir sınıfa atanır. Alternatif olarak, yaprak, hedef özelliğin belirli bir değere sahip olma olasılığını gösteren bir olasılık vektörü tutabilir. Örnekler, yol boyunca yapılan testlerin sonucuna göre, onları ağacın kökünden bir yaprağa götürerek sınıflandırılır. Şekil 1, potansiyel bir müşterinin doğrudan postalamaya yanıt verip vermeyeceğini açıklayan bir karar ağacını açıklamaktadır. İç düğümler daire ile temsil edilirken, yapraklar üçgenler ile gösterilir. [3]
Bu karar ağacının hem nominal hem de sayısal özellikleri içerdiğine dikkat edin. Bu sınıflandırıcı göz önüne alındığında, analist potansiyel bir müşterinin tepkisini tahmin edebilir (ağacı sıralayarak) ve doğrudan postayla ilgili tüm potansiyel müşteri populasyonunun davranış özelliklerini anlayabilir [3].
Her düğüm test ettiği öz nitelikle etiketlenir ve dalları karşılık gelen değerleriyle etiketlenir [3].

Şekil 1 deki yollar kurala dönüşebilir. Müşterinin yaşı 30da büyük ise postaya yanıt vermeyecektir.
Bir diğer kuralı da şu şekilde belirtebiliriz: Müşterinin yaşı 30 a eşit veya küçük ise ve müşterinin cinsiyeti erkek ise müşteri postaya yanıt verecektir.
Ortaya çıkan kural kümesi daha sonra bir insan kullanıcı için anlaşılabilirliğini ve muhtemelen doğruluğunu geliştirmek için basitleştirilebilir [4].
2.1 Bölme Kıstası
Bölme kriterinin amacı, farklı sınıfların alt düğümler arasındaki ayrımını en üst düzeye çıkarmaktır. Aşağıda, sadece tek değişkenli kriterler tanımlanmıştır. Bir bölünmeyi değerlendirmek için bir kalite kriterinin mevcut olduğunu varsayalım. Bölünmüş kriterin tasarımı, temeldeki niteliğinin doğasına bağlıdır[1]:
- İkili öznitelik: Yalnızca bir tür bölme mümkündür ve ağaç her zaman ikilidir. Her dal, ikili değerlerden birine karşılık gelir.
- Kategorik öznitelik: Kategorik bir özniteliğin r farklı değeri varsa, onu bölmenin birçok yolu vardır. Bir olasılık, bölünmenin her bir dalının belirli bir öznitelik değerine karşılık geldiği bir r-yollu bölme kullanmaktır. Diğer olasılık, kategorik özelliklerin 2r – 1 kombinasyonlarının (veya gruplamalarının) her birini test ederek ve en iyisini seçerek bir ikili bölme kullanmaktır. Açıkçası, r’nin değeri büyük olduğunda bu uygulanabilir bir seçenek değildir. Bazen kullanılan basit bir yaklaşım, ikilileştirme yaklaşımını kullanarak kategorik verileri ikili verilere dönüştürmektir. Bu durumda, ikili öznitelikler için yaklaşım kullanılabilir.
- Sayısal öznitelik: Sayısal öznitelik az sayıda sıralı değer içeriyorsa (örneğin, küçük bir aralıktaki [1, r] tam sayılar), her bir farklı değer için bir r-yolu bölmesi oluşturmak mümkündür. Bununla birlikte, sürekli sayısal öznitelikler için, bölme tipik olarak öznitelik değeri x ve sabit a için x ≤ a gibi bir ikili koşul kullanılarak gerçekleştirilir.
Yukarıda bahsedilen yöntemlerin çoğu, bir dizi seçenekten “en iyi” ayrımın belirlenmesini gerektirir. Spesifik olarak, her bir özniteliği bölmek için mevcut çeşitli alternatifler ve birden çok öznitelik arasından seçim yapılması gerekir. Bu nedenle, bölünmüş kalite miktarlarının belirlenmesi gereklidir. Bu miktarlar, özellik seçim kriterleri ile aynı ilkelere dayanmaktadır: [1]
2.1.1. Gini Endeksi
Bir dizi S veri noktası için Gini indeksi G (S), S ‘deki eğitim veri noktalarının p1….pk’si sınıf dağılımı üzerinde hesaplanabilir. [1]
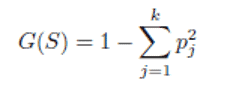
S kümesinin S1 kümelerine r-yollu bölünmesi için genel Gini indeksi. . . Sr, Si’nin ağırlığının | Si | olduğu her Si’nin Gini indeksi değerlerinin G (Si) ağırlıklı ortalaması olarak ölçülebilir. [1]
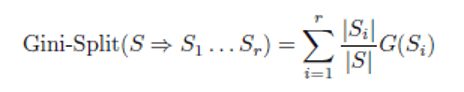
2.1.1. Entropi
Entropi ölçümü, ID3 olarak adlandırılan en eski sınıflandırma algoritmalarından birinde kullanılır. [1]
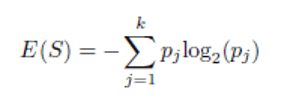
Gini indeksinde olduğu gibi, S kümesinin S1 kümelerine r-yollu bölünmesi için genel entropi. . . Sr, Si’nin ağırlığının | Si | olduğu her Si’nin Gini indeksi değerlerinin G (Si) ağırlıklı ortalaması olarak hesaplanabilir.
Entropinin daha düşük değerleri daha çok arzu edilir. Entropi ölçümü, ID3 ve C4.5 algoritmaları tarafından kullanılır. [1].
Bilgi kazancı entropi ile yakından ilişkilidir ve bölünmenin bir sonucu olarak entropi E (S) – Entropi-Bölünmüş (S ⇒ S1.. Sr) azalmasına eşittir. Büyük indirgeme değerleri arzu edilir. Kavramsal düzeyde, ikisinin ikisinin de bir bölünme için kullanılması arasında bir fark yoktur, ancak bilgi kazanımı durumunda bölünme derecesi için bir normalizasyon mümkündür. Entropi ve bilgi kazancı ölçümlerinin yalnızca aynı derecedeki iki bölünmeyi karşılaştırmak için kullanılması gerektiğine dikkat edin, çünkü her iki ölçüm de doğal olarak daha büyük dereceli bölünmeler lehine önyargılıdır. Örneğin, kategorik bir özniteliğin birçok değeri varsa, çok değerli öznitelikler tercih edilecektir.
Örneğin, kategorik bir özniteliğin birçok değeri varsa, çok değerli öznitelikler tercih edilecektir. C4.5 algoritması, genel bilgi kazancını nin normalleştirme faktörüne bölmenin değişen sayıdaki kategorik değerlerin ayarlanmasına yardımcı olduğu gösterilmiştir [1].
Örneğin, sayısal bir veritabanı durumunda, her sayısal öznitelik için farklı bölme noktaları test edilir ve en iyi bölme seçilir [1].
2.2 Popüler Karar Ağacı Algoritmaları
2.2.1. ID3 Algortiması
ID3 algoritması çok basit bir karar ağacı algoritması olarak kabul edilir [7]. Bilgi kazancını bir bölme kriteri olarak kullanan ID3 algoritması, tüm örnekler bir hedef özelliğin tek bir değerine ait olduğunda veya en iyi bilgi kazancı sıfırdan büyük olmadığında büyümeyi durdurur. ID3 herhangi bir budama prosedürü uygulamaz ve sayısal nitelikleri veya eksik değerleri işlemez. ID3’ün temel avantajı basitliğidir. Bu nedenle ID3 algoritması öğretim amacıyla sıklıkla kullanılmaktadır [8].
2.2.2. C4.5 Algortiması
Aynı yazar tarafından sunulan ID3’ün bir evrimi olan C4.5, bölme kriteri olarak kazanç oranını kullanır. [9]. Bölünecek örnek sayısı belirli bir eşiğin altına düştüğünde bölme durur. Büyüme aşamasından sonra hataya dayalı budama yapılır. C4.5 sayısal öznitelikleri işleyebilir [8].
C4.5 algoritması, ID3’e çeşitli iyileştirmeler sağlar. En önemli iyileştirmeler [8]:
- 5, doğruluğa katkıda bulunmayan dalları kaldıran ve bunları yaprak düğümlerle değiştiren bir budama prosedürü kullanır.
- 5, nitelik değerlerinin eksik olmasına izin verir (? Olarak işaretlenir).
- 5, özniteliğin değer aralığını iki alt kümeye (ikili bölme) bölerek sürekli öznitelikleri yönetir. Spesifik olarak, kazanç oranı kriterini maksimize eden en iyi eşiği arar. Eşiğin üzerindeki tüm değerler ilk alt kümeyi ve diğer tüm değerler ikinci alt kümeyi oluşturur.
2.2.Karar Ağaçlarının Avantaj ve Dezavantajları
Karar ağacının bir sınıflandırma aracı olarak çeşitli avantajları literatürde belirtilmiştir [8]:
- Karar ağaçları kendiliğinden açıklayıcıdır ve sıkıştırıldıklarında izlemeleri de kolaydır. Diğer bir deyişle, karar ağacının makul sayıda izni varsa, profesyonel olmayan kullanıcılar tarafından kavranabilir. Ayrıca karar ağaçları bir dizi kurala dönüştürülebilir. Dolayısıyla bu temsilin anlaşılabilir olduğu düşünülmektedir.
- Karar ağaçları hem nominal hem de sayısal girdi özniteliklerini işleyebilir.
- Karar ağacı temsili, herhangi bir ayrık değer sınıflandırıcısını temsil edecek kadar zengindir.
- Karar ağaçları, hatalı olabilecek veri kümelerini işleyebilir.
- Karar ağaçları, eksik değerlere sahip olabilecek veri kümelerini işleme yeteneğine sahiptir.
- Karar ağaçları parametrik olmayan bir yöntem olarak kabul edilir. Bu, karar ağaçlarının alan dağılımı ve sınıflandırıcı yapısı hakkında hiçbir varsayımının olmadığı anlamına gelir.
- Sınıflandırma maliyeti yüksek olduğunda, karar ağaçları sadece kökten yaprağa tek bir yoldaki özelliklerin değerlerini talep etmeleri açısından çekici olabilir.
Öte yandan, karar ağaçlarının şu gibi dezavantajları vardır [8]:
- Algoritmaların çoğu (ID3 ve C4.5 gibi), hedef özelliğin yalnızca ayrı değerlere sahip olmasını gerektirir.
- Karar ağaçları “böl ve yönet” yöntemini kullandıklarından, oldukça alakalı birkaç özellik varsa iyi performans gösterme eğilimindedirler, ancak birçok karmaşık etkileşim varsa daha az performans gösterirler. Bunun nedenlerinden biri, diğer sınıflandırıcıların, bir karar ağacı kullanarak temsil etmesi çok zor olacak bir sınıflandırıcıyı kompakt bir şekilde tanımlayabilmesidir.
Çoğu karar ağacı, bir kavramı temsil etmek için örnek alanını birbirini dışlayan bölgelere böldüğünden, bazı durumlarda ağaç, sınıflandırıcıyı temsil etmek için aynı alt ağacın birkaç kopyasını içerir. Örneğin, kavram aşağıdaki ikili işlevi izlerse: y = (A1 \ A2) [(A3 \ A4) bu işlevi temsil eden minimum tek değişkenli karar ağacı Şekil 2’de gösterilmektedir Ağacın aynı alt satırın iki kopyasını içerdiğine dikkat edilmelidir.
3.Karar ağaçlarının açgözlü özelliği, belirtilmesi gereken başka bir dezavantaja yol açar. Bu, eğitim setine, ilgisiz niteliklere karşı aşırı duyarlılığı karar ağaçlarını özellikle istikrarsız hale getirir: köke yakın bir bölünmede küçük bir değişiklik aşağıdaki tüm alt ağacı değiştirecektir [9].
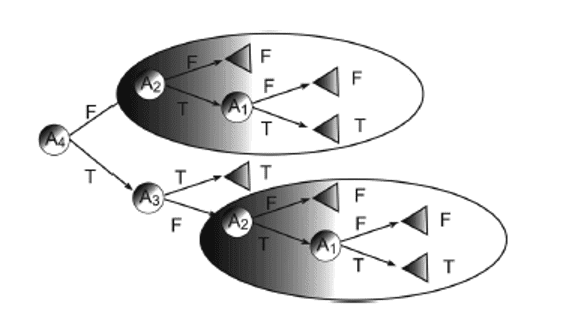
- Parçalanma sorunu, verilerin daha küçük parçalara bölünmesine neden olur. Bu genellikle yol boyunca birçok özellik test edilirse gerçekleşir. Veriler her bölünmede yaklaşık olarak eşit olarak bölünüyorsa, tek değişkenli bir karar ağacı O (logn) özelliklerinden fazlasını test edemez. Bu, birçok ilgili özelliğe sahip görevler için karar ağaçlarını dezavantajlı konuma getirir. Çoğaltmanın her zaman parçalanma anlamına geldiğini, ancak parçalanmanın herhangi bir çoğaltma olmadan gerçekleşebileceği unutulmamalıdır.
- Diğer bir problem, eksik değerlerle başa çıkmak için gereken eforla ilgilidir [15]. Eksik değerleri ele alma becerisi bir avantaj olarak kabul edilirken, bunu başarmak için gereken aşırı çaba bir dezavantaj olarak kabul edilir. Test edilen bir özellik eksikse alınacak doğru dal bilinmemektedir ve algoritmanın eksik değerleri işlemek için özel mekanizmalar kullanması gerekir. C4.5, eksik değerler üzerindeki test oluşumlarını azaltmak için, bilgi kazanımını bilinmeyen vakaların oranıyla cezalandırır ve ardından bu örnekleri alt ağaçlara böler. CART, yerine geçen özelliklerin çok daha karmaşık bir şemasını kullanır.
3-Uygulama
Bu uygulamada ID3 / C4.5 uygulanacaktır. Bir şirketin A,B,C ürünleri ile ilgili satış detayları verilmiştir. Bu ürünler ile beraber aşağıda belirlenen özelliklerde ürünler ile beraber aksesuar alma kararı da sette tanımlanmıştır.
Örneğin; A ürün tipi 5 ten az sayıdaki alımlar için düşük cirolu bir müşteri tarafından yurtiçinde kullanılmak üzere aksesuarsız olarak alınmıştır.
| No | Tip | Ürün Sayısı | Ciro | Yurtiçi | Aksesuar |
| 1 | A | <=5 | düşük | evet | hayır |
| 2 | A | <=5 | düşük | evet | hayır |
| 3 | B | 5…10 | orta | evet | evet |
| 4 | A | <=5 | orta | evet | hayır |
| 5 | A | <=5 | yüksek | evet | hayır |
| 6 | B | >10 | orta | evet | evet |
| 7 | A | <=5 | orta | evet | evet |
| 8 | A | <=5 | orta | evet | hayır |
| 9 | C | <=5 | orta | evet | evet |
| 10 | B | <=5 | yüksek | hayır | hayır |
| 11 | B | <=5 | yüksek | hayır | hayır |
| 12 | B | <=5 | yüksek | evet | evet |
| 13 | A | <=5 | düşük | evet | hayır |
| 14 | A | <=5 | düşük | evet | evet |
| 15 | B | 5…10 | yüksek | hayır | hayır |
| 16 | A | <=5 | yüksek | hayır | evet |
| 17 | C | <=5 | yüksek | hayır | hayır |
| 18 | C | <=5 | yüksek | hayır | hayır |
| 19 | C | 5…10 | yüksek | hayır | hayır |
| 20 | B | <=5 | yüksek | hayır | hayır |
| 21 | A | <=5 | yüksek | hayır | hayır |
| 22 | A | <=5 | yüksek | hayır | hayır |
| 23 | C | <=5 | yüksek | evet | evet |
| 24 | B | <=5 | düşük | evet | evet |
| 25 | C | <=5 | orta | evet | evet |
| 26 | C | <=5 | orta | evet | evet |
| 27 | A | 5…10 | orta | evet | hayır |
| 28 | B | 5…10 | yüksek | hayır | hayır |
| 29 | B | 5…10 | yüksek | hayır | hayır |
| 30 | C | <=5 | düşük | evet | evet |
| 31 | B | 5…10 | yüksek | hayır | hayır |
| 32 | C | <=5 | orta | evet | evet |
| 33 | B | <=5 | orta | hayır | hayır |
| 34 | B | <=5 | orta | hayır | hayır |
| 35 | A | <=5 | orta | hayır | hayır |
| 36 | A | 5…10 | orta | evet | hayır |
| 37 | B | >10 | orta | evet | evet |
| 38 | C | <=5 | orta | evet | evet |
| 39 | C | <=5 | orta | evet | evet |
| 40 | A | <=5 | orta | evet | hayır |
| 41 | C | <=5 | düşük | evet | evet |
| 42 | A | <=5 | orta | evet | hayır |
| 43 | C | <=5 | orta | evet | evet |
| 44 | B | <=5 | orta | evet | evet |
| 45 | A | <=5 | orta | evet | hayır |
| 46 | B | <=5 | düşük | evet | evet |
| 47 | A | <=5 | yüksek | evet | hayır |
| 48 | B | 5…10 | düşük | hayır | hayır |
| 49 | B | 5…10 | orta | evet | evet |
| 50 | A | <=5 | yüksek | hayır | hayır |
| 51 | A | <=5 | yüksek | evet | evet |
| 52 | A | <=5 | yüksek | hayır | evet |
| 53 | B | 5…10 | yüksek | hayır | hayır |
| 54 | A | <=5 | düşük | evet | hayır |
| 55 | A | <=5 | yüksek | hayır | hayır |
| 56 | A | <=5 | yüksek | evet | hayır |
| 57 | C | >10 | yüksek | hayır | hayır |
| 58 | B | <=5 | orta | hayır | hayır |
| 59 | B | >10 | yüksek | evet | evet |
| 60 | A | <=5 | orta | evet | evet |
| 61 | A | <=5 | düşük | evet | evet |
| 62 | C | >10 | yüksek | hayır | hayır |
| 63 | A | <=5 | yüksek | hayır | hayır |
P = Aksesuarlı ürün alma “evet” = 26
N= Aksesuarlı ürün alma “hayır” = 37
İlk ayrılmayı bulabilmek için bilgi kazancı formülü kullanılarak tüm seçenekler için hesaplama yapılır.
| Tip | pi | ni | I(pi,ni) |
| A | 7 | 20 | 0,8256265 |
| B | 9 | 12 | 0,9852281 |
| C | 10 | 5 | 0,9182958 |
| Ürün Sayısı | pi | ni | I(pi,ni) |
| <=5 | 21 | 26 | 0,9918208 |
| 5…10 | 2 | 9 | 0,6840384 |
| >10 | 3 | 2 | 0,9709506 |
| Ciro | pi | ni | I(pi,ni) |
| Düşük | 6 | 5 | 0,9940302 |
| Orta | 14 | 11 | 0,9895875 |
| Yüksek | 6 | 21 | 0,7642045 |
| Yurtiçi | pi | ni | I(pi,ni) |
| Evet | 24 | 14 | 0,949452 |
| Hayır | 2 | 23 | 0,4021792 |

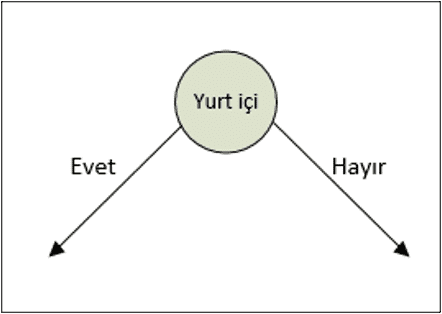
Bu hesaplamalara göre en yüksek kazanca sahip satr özelliği ilk bölünme ayrımı olarak seçilir. Bu da karar ağacımızda yurtiçi evet ve yurtiçi hayır olmak üzere 2 ayrı kol oluşturur.
Tabloda yurtiçi evet ve yurt içi hayır seçenekleri seçilerek iki ayrı tablo oluşturulur ve bu kollar için kazanç tekrar hesaplanır.
Bu aşamada karar ağacı aşağıdaki şekildedir:
Tüm kollar için hesaplamalar tekrarlanarak en son bölünme noktası bulunana kadar hesaplama yapılmaya devam edilir.
Yurtiçi bölünmesi için “evet” kolu :
| No | Yurtiçi | Tip | Ürün Sayısı | Ciro | Aksesuar |
| 1 | Evet | A | <=5 | Düşük | Hayır |
| 2 | Evet | A | <=5 | Düşük | Hayır |
| 3 | Evet | B | 5…10 | Orta | Evet |
| 4 | Evet | A | <=5 | Orta | Hayır |
| 5 | Evet | A | <=5 | Yüksek | Hayır |
| 6 | Evet | B | >10 | Orta | Evet |
| 7 | Evet | A | <=5 | Orta | Evet |
| 8 | Evet | A | <=5 | Orta | Hayır |
| 9 | Evet | C | <=5 | Orta | Evet |
| 10 | Evet | B | <=5 | Yüksek | Evet |
| 11 | Evet | A | <=5 | Düşük | Hayır |
| 12 | Evet | A | <=5 | Düşük | Evet |
| 13 | Evet | C | <=5 | Yüksek | Evet |
| 14 | Evet | B | <=5 | Düşük | Evet |
| 15 | Evet | C | <=5 | Orta | Evet |
| 16 | Evet | C | <=5 | Orta | Evet |
| 17 | Evet | A | 5…10 | Orta | Hayır |
| 18 | Evet | C | <=5 | Düşük | Evet |
| 19 | Evet | C | <=5 | Orta | Evet |
| 20 | Evet | A | 5…10 | Orta | Hayır |
| 21 | Evet | B | >10 | Orta | Evet |
| 22 | Evet | C | <=5 | Orta | Evet |
| 23 | Evet | C | <=5 | Orta | Evet |
| 24 | Evet | A | <=5 | Orta | Hayır |
| 25 | Evet | C | <=5 | Düşük | Evet |
| 26 | Evet | A | <=5 | Orta | Hayır |
| 27 | Evet | C | <=5 | Orta | Evet |
| 28 | Evet | B | <=5 | Orta | Evet |
| 29 | Evet | A | <=5 | Orta | Hayır |
| 30 | Evet | B | <=5 | Düşük | Evet |
| 31 | Evet | A | <=5 | Yüksek | Hayır |
| 32 | Evet | B | 5…10 | Orta | Evet |
| 33 | Evet | A | <=5 | Yüksek | Evet |
| 34 | Evet | A | <=5 | Düşük | Hayır |
| 35 | Evet | A | <=5 | Yüksek | Hayır |
| 36 | Evet | B | >10 | Yüksek | Evet |
| 37 | Evet | A | <=5 | Orta | Evet |
| 38 | Evet | A | <=5 | Düşük | Evet |
P = Aksesuarlı ürün alma “evet” = 24
N= Aksesuarlı ürün alma “hayır” = 14
| Tip | pi | ni | I(pi,ni) |
| A | 5 | 14 | 0,8314744 |
| B | 9 | 0 | 0 |
| C | 10 | 0 | 0 |
| Ürün Sayısı | pi | ni | I(pi,ni) |
| <=5 | 19 | 12 | 0,9629004 |
| 5…10 | 2 | 2 | 1 |
| >10 | 3 | 0 | 0 |
| Ciro | pi | ni | I(pi,ni) |
| Düşük | 6 | 4 | 0,9709506 |
| Orta | 14 | 7 | 0,9182958 |
| Yüksek | 4 | 3 | 0,9852281 |

Burada en yüksek kazanç seçilir. En yüksek kazanç tip seçeneğinde bulunmaktadır. Artık kollarımızında bu tip seçeneğine göre ayrılmış olduğunu bulduk. (A, B, C)
Şu ana kadar hesapladıklarımız ile karar ağacının şekli aşağıdaki gibi oluşmuştur:
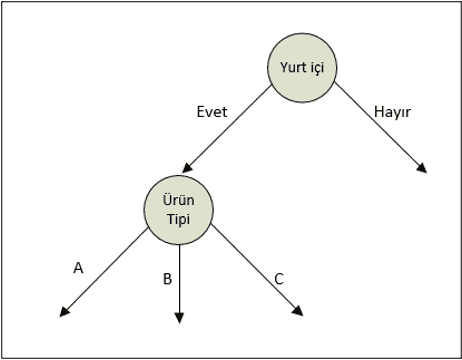
B ve C Ürün tipi listelendiğinde, Aksesuar alma kararının direkt Evet olduğu görülecektir. A ürün tipi için ise bilgi kazancı hesaplanmaya devam edilir.
| Yurtiçi | Tip | Ürün Sayısı | Ciro | Aksesuar |
| Evet | A | <=5 | Düşük | Hayır |
| Evet | A | <=5 | Düşük | Hayır |
| Evet | A | <=5 | Orta | Hayır |
| Evet | A | <=5 | Yüksek | Hayır |
| Evet | A | <=5 | Orta | Evet |
| Evet | A | <=5 | Orta | Hayır |
| Evet | A | <=5 | Düşük | Hayır |
| Evet | A | <=5 | Düşük | Evet |
| Evet | A | 5…10 | Orta | Hayır |
| Evet | A | 5…10 | Orta | Hayır |
| Evet | A | <=5 | Orta | Hayır |
| Evet | A | <=5 | Orta | Hayır |
| Evet | A | <=5 | Orta | Hayır |
| Evet | A | <=5 | Yüksek | Hayır |
| Evet | A | <=5 | Yüksek | Evet |
| Evet | A | <=5 | Düşük | Hayır |
| Evet | A | <=5 | Yüksek | Hayır |
| Evet | A | <=5 | Orta | Evet |
| Evet | A | <=5 | Düşük | Evet |
P = Aksesuarlı ürün alma “evet” = 5
N= Aksesuarlı ürün alma “hayır” = 14
| Ürün Sayısı | pi | ni | I(pi,ni) |
| <=5 | 5 | 12 | 0,873981 |
| 5…10 | 0 | 2 | 0 |
| >10 | 0 | 0 | 0 |
| Ciro | pi | ni | I(pi,ni) |
| Düşük | 2 | 4 | 0,9182958 |
| Orta | 2 | 7 | 0,7642045 |
| Yüksek | 1 | 3 | 0,8112781
|

En yüksek kazanç seçilerek bu hesaplamaya ve kol ayırmaya devam edilir.
Sonuç olarak karar ağacı aşağıdaki şekilde oluşur:

Yukarıdaki karar ağacına göre aşağıdaki kararlar oluşturulabilir: Ürün tipi A ve B için tüm yurt içi siparişleri aksesuar almaktadır. Ürün tipi A ve B için yurtdışı siparişlerinde aksesuar satışı yapılmamaktadır. 5-10 ürün sayısına sahip yurtiçi siparişlerinde C ürün tipinde aksesuar satılmamaktadır.
4-Sonuç
Bu makale karar ağaçlarının tanımlarını, avantajlarını ve dezavantajlarını sunmaktadır.
Ayrıca, bu makalede avantajları ve dezavantajları ile ID3, C4.5 algoritmalı karar ağacı yaklaşımları vermektedir;. ID3’ün temel avantajı basitliğidir. Bu nedenle ID3 algoritması öğretim amaçlı sıklıkla kullanılmaktadır. C4.5 algoritması, ID3’ün bir evrimidir ve bu, bölme kriteri olarak kazanç oranını kullanır. Yazının 3. Bölümünde ise ID3 kullanılarak veri seti üzerinde karar ağacı oluşturulması yöntemi tanımlanmıştır.
5-Referanslar
- [1] Aggarwal, C. C. (2015). Data mining: the textbook
- [2] Bhargava, N., Sharma, G., Bhargava, R., & Mathuria, M. (2013). Decision tree analysis on j48 algorithm for data mining. Proceedings of International Journal of Advanced Research in Computer Science and Software Engineering, 3(6).
- [3] Rokach, L., & Maimon, O. (2005). Decision trees. In Data mining and knowledge discovery handbook (pp. 165-192). Springer, Boston, MA.
- [4] Quinlan, J.R., Simplifying decision trees, International Journal of Man-Machine Studies, 27, 221-234, 1987.
- [5] Breiman, L., Friedman, J., Olshen, R., & Stone, C. (1984). Classification and regression trees. Wadsworth Int. Group, 37(15), 237-251.
- [6] Rokach, L., & Maimon, O. Z. (2008). Data mining with decision trees: theory and applications (Vol. 69). World scientific.
- [7] Quinlan J. R., Induction of decision trees, Machine Learning 1:81–106, 1986.
- [8] Rokach, L., & Maimon, O. (2015). Data mining with decision trees–Theory and Applications 2nd Edition. Series in Machine Perception and Artificial Intelligence, 81, 328.
- [9] Quinlan, J. R., C4.5: Programs for Machine Learning, Morgan Kaufmann, Los Altos, 1993.
- [10] Moore S. A., Daddario D. M., Kurinskas J. and Weiss G. M., Are decision trees always greener on the open (source) side of the fence?, Proceedings of DMIN, pp. 185–188, 2009.
- [11] Kass G. V., An exploratory technique for investigating large quantities of categorical data, Applied Statistics 29(2):119–127, 1980.
- [12] IBM SPSS Decision Trees 19 by SPSS Inc. 1989, 2010.
- [13] Loh W. Y., and Shih X., Split selection methods for classification trees, Statistica Sinica 7:815–840, 1997.
- [14] Pagallo, G. and Huassler, D., Boolean feature discovery in empirical learning, Machine Learning, 5(1): 71-99, 1990.
- [15] Friedman, J., Kohavi, R., Yun, Y. 1996. Lazy decision trees. Proceedings of the Thirteenth National Conference on Artificial Intelligence. (pp. 717-724).


